This post is based on joint work with Gianira N. Alfarano.
Last June, Mark Saaltink wrote on this blog about the q-analogue of transversal matroids. Key to this definition is the rather ingenious idea to not consider transversals, but avoiding transversals. This post explores this idea further. Our goal is to sketch a proof for Saaltink’s conjecture that every (avoiding) transversal q-matroid has a unique minimal presentation. However, we will ignore the q-analogue most of the time, because the setting is also valid for plain old transversal matroids. We describe what appears to be a new algorithm to find maximal / minimal presentations.
Cyclic sets and flats
Before we consider transversals, a quick recap of flats and cyclic sets. Consider a matroid with ground set $E$. The closure operator $\mathop{cl} : 2^E \to 2^E$ is defined by
\[ \mathop{cl}(X) = \{e \in E : r(X \cup e) = r(X)\}, \]
and the cyclic operator $\mathop{cyc} : 2^E \to 2^E$ is defined by
\[ \mathop{cyc}(X) = \{e \in X : r(X \setminus{e}) = r(X)\}.\]
For every $X\in 2^E$, we say that $\mathop{cl}(X)$ is the closure of $X$ and $\mathop{cyc}(X)$ is the cyclic core of $X$. A subset $X \subseteq E$ is a flat if $\mathop{cl}(X) = X$ and a cyclic set if $\mathop{cyc}(X) = X$. Therefore, $X$ is a cyclic flat if for all $y \in E\setminus X$ and $x \in X$,
\[ r(X \cup y) > r(X) \quad \text{and} \quad r(X \setminus {x}) = r(X). \]
Both the closure and the cyclic core are uniquely defined. To find the closure of a set, simply keep adding elements until adding any other element will increase the rank. For the cyclic closure, take away elements such that the rank decreases until there are only elements left that, when deleted, will not change the rank.
It is well known that closure and cyclic core are dual operations: the complement of the closure of a set is the cyclic core of the complement of this set in the dual matroid. We mention also the following.
Lemma. For any set $X\subseteq E$, we have that both $\mathop{cyc}(\mathop{cl}(X))$ and $\mathop{cl}(\mathop{cyc}(X))$ are cyclic flats. In particular, both the cyclic core of a flat and the closure of a cyclic set are cyclic flats.
Avoiding transversals
The definition of an avoiding transversal is due to Saaltink [Saa2025].
Definition. Given an indexed family $\mathcal{X}=(X_1,\ldots,X_k)$ of subsets of some given set $E$, an avoiding transversal of $ \mathcal{X}$ is a set of elements $x_1,x_2,\ldots,x_k$ of $E$, all distinct, with each $x_i\notin X_i$. A partial avoiding transversal of $\mathcal{X}$ is an avoiding transversal of some subfamily of $\mathcal{X}$.
We can make a matroid out of every avoiding transversal.
Theorem. Let $\mathcal{X}$ be an avoiding transversal of a finite set $E$. Then the set of avoiding transversals of $\mathcal{X}$ forms the set of bases of a matroid with ground set $E$.
Let $X_i=E\setminus A_i$. Since every avoiding transversal of $\mathcal{X}=(X_1,\ldots,X_k)$ is a transversal of $\mathcal{A}=(A_1,A_2,\ldots,A_k)$, the class of transversal matroids and the class of avoiding transversal matroids are the same. In the q-analogue, only the class of avoiding transversal q-matroids has a sensible definition. (Saaltink uses the term “transversal q-matroids” for them; we add “avoiding” here to emphasise the link with avoiding transversals and remove confusion.) This is why in the search for more results about q-analogues of transversal matroids, one needs to study avoiding transversals.
Presentations
When the independent sets of a matroid are exactly the partial transversals of $\mathcal{A}=(A_1,A_2,\ldots,A_k)$, we call $\mathcal{A}$ a presentation of $M$. (We will assume that all presentations contain $r(M)=k$ sets.) The representation of a transversal matroid is not necessarily unique, as the next result shows.
Proposition A. Let $\mathcal{A} = (A_1, A_2, \ldots , A_k )$ be a presentation of the transversal matroid $M$ of rank $k$, and let $a\in E\setminus A_1$. Then $\mathcal{A}’ = (A_1\cup \{a\}, A_2, \ldots , A_k )$ is also a presentation of $M$ if and only if $a$ is an isthmus of the restriction $M|(E \setminus A_1)$.
This proposition is due to [BW1971]. If we can add isthmusses to presentations without changing the corresponding matroid, the question arises if a matroid has a maximal presentation, that is, a presentation where adding any element to one of its subsets gives a new matroid. The answer is yes, as was first shown in [Mas1969] and [Bon1972]. Proposition A is a first step in proving this. We will see that the rest of the proof is immediate if we translate Proposition A to avoiding transversals. First, we need a definition.
Definition. Given $A\subseteq E$, we say that a subset $H\subseteq A$ with $|H|=|A|-1$ is a non-spanning $(|A|-1)$-set if it does not contain any basis of $M|A$.
This definition might feel overly complicated and in a sense, it is: a non-spanning $(|E|-1)$-set is the complement of an isthmus. However, with an eye on the q-analogue, we want to avoid isthmusses, because in the q-analogue they do not exist (that is, there can be no 1-dimensional space contained in every basis; see Lemma 5.4 of [JPR2025]). But we can talk about non-spanning $(\dim(E)-1)$-spaces.
We can now translate Proposition A to avoiding transversals.
Proposition B. Let $\mathcal{X} = (X_1, X_2, \ldots , X_k )$ be a presentation of the avoiding transversal matroid $M$ of rank $k$, and let $A\subseteq X_1$ of size $|X_1|-1$. Then $\mathcal{X}’ = (X_1\cap A, X_2, \ldots , X_k )$ is also a presentation of $M$ if and only if $A$ is a non-spanning $(|X_1|-1)$-set of the restriction $M|X_1$.
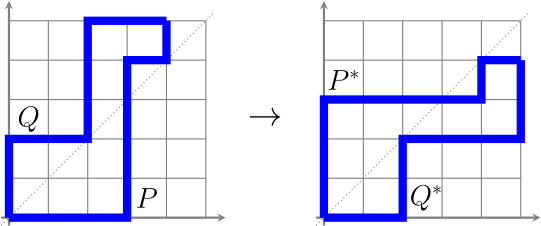
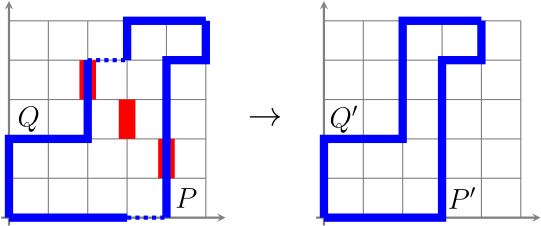
This point of view now gives us a direct proof of the existence and uniqueness of a minimal presentation of an avoiding transversal matroid: simply take the cyclic core of every set in the presentation! Indeed, intersecting with a non-spanning $(|A|-1)$-set repeatedly produces the cyclic core of a set.
With some extra taking of complements, we can find the maximal representation of a transversal matroid, as we illustrate with an example. It comes from exercise 3 op p.47 of [Oxl2011].
Example. Let $E=\{1,2,3,4,5,6\}$ and $\mathcal{A}=(A_1,A_2,A_3)$ where $A_1=\{1,2,3\}$, $A_2=\{2,3,4\}$ and $A_3=\{4,5,6\}$. The cyclic flats of $M$ are $\emptyset$, $\{5,6\}$, $\{1,2,3\}$ and $E$.
Now $M$ can also be viewed as the avoiding transversal matroid corresponding to $\mathcal{X}=(\{4,5,6\},\{1,5,6\},\{1,2,3\})$. Taking the cyclic core of these subsets gives that $\mathcal{X}’=(\{5,6\},\{5,6\},\{1,2,3\})$ is a minimal presentation of $M$ as an avoiding transversal matroid. Hence, $\mathcal{A}’=(\{1,2,3,4\},\{1,2,3,4\},\{4,5,6\})$ is a maximal presentation of $M$ as a transversal matroid.
This leads us to the question: is this a known procedure to obtain a maximal presentation? Classic texts like [Bru1987] and [BKdM2011] do not mention the cyclic core, but use a much more involved procedure that requires knowing not only the cyclic flats, but also their ranks, and calculating a function that gives the multiplicity of these cyclic flats in the maximal presentation. It feels like the procedure as in the Example is much shorter. Please let us know if we are re-inventing the wheel! We admit to having read only a fraction of the literature on transversal matroids.
Finally, we can now prove Saaltink’s conjecture, because we have exactly the same results for avoiding transversal q-matroids. We can first prove Proposition B by taking a lot of complements in the proof of Proposition A. This is a non-trivial task! But as a result, we get a proof that has a straightforward q-analogue. The conjecture then follows by the same reasoning as above.
Theorem. Let $(X_1,X_2,\ldots,X_k)$ be a presentation of the avoiding transversal q-matroid $M$. Then $(\mathop{cyc}(X_1),\mathop{cyc}(X_2),\ldots,\mathop{cyc}(X_k))$ is the unique minimal presentation of $M$.
References
[BKdM2011] J.E. Bonin, J.P.S. Kung and A. de Mier. Characterizations of Transversal and Fundamental Transversal Matroids. Electronic Journal of Combinatorics, 18(1): P106, 2011.
[Bon1972] J.A. Bondy. Presentations of transversal matroids, Journal of the London Mathematical Society, 5(2): 289-292, 1972.
[Bru1987] R.A. Brualdi. Transversal matroids. In: N. White, editor, Combinatorial geometries, pages 72–97, Cambridge University Press, Cambridge, 1987.
[BW1971] J.A. Bondy and D.J.A. Welsh. Some results on transversal matroids and constructions for identically self-dual matroids, Quarterly Journal of Mathematics, 22(3): 435-451, 1971.
[JPR2025] T. Johnsen, R. Pratihar and T. H. Randrianarisoa. The Euler characteristic, q-matroids, and a Möbius function. Journal of Algebra and Its Applications, 2025.
[Mas1969] J. Mason. Representations of independent spaces. PhD dissertation, University of Wisconsin, Madison WI, 1969.
[Oxl2011] J.G. Oxley. Matroid Theory. Oxford University Press, USA, 2011.
[Saa2025] M. Saaltink. A theory of q-transversals. arXiv:2503.12201, 2025.