From lattice paths to matroids

Lattice paths and Catalan numbers were some of the favourite topics in my recent combinatorics course. And while we didn’t cover them in class, I was reminded of lattice path matroids.

The systematic study of lattice path matroids was initiated by Joe Bonin, Anna de Mier, and Marc Noy. The results I describe here (as well as their proofs) can all be found in this paper by Bonin and De Mier.

A north-east lattice path (I will call them lattice paths for simplicity) is a sequence $v_0 = (0,0), v_1, \ldots, v_\ell$ of points in the lattice $\mathbb{Z}^2$ such that each step $P_i = v_i – v_{i-1}$ is either in the east direction $E = (1,0)$ or in the north direction $N = (0,1)$. As such lattice paths always start at the origin, they are in one-to-one correspondence with words over the alphabet $\{E,N\}$.

There are exactly $\binom{a+b}{b}$ lattice paths to $(a,b)$, as all such paths have $a+b$ steps, and identifying the $b$ north steps among them suffices to describe the path.

Given a lattice path $P$ to $(a,b)$, written as a sequence $P_1P_2\ldots P_{a+b}$ of $a$ east steps and $b$ north steps, we can record the north steps as follows: $$\mathcal{N}(P) = \{i : P_i = N\}.$$

All $b$-element subsets of $[a+b]$ appear as $\mathcal{N}(P)$ for some lattice path $P$ to $(a,b)$; in other words, the set of all $\mathcal{N}(P)$, as $P$ ranges over the lattice paths to $(a,b)$, is the set of bases of the rank-$b$ uniform matroid on $[a+b]$. Lattice path matroids generalise this construction.

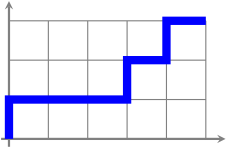
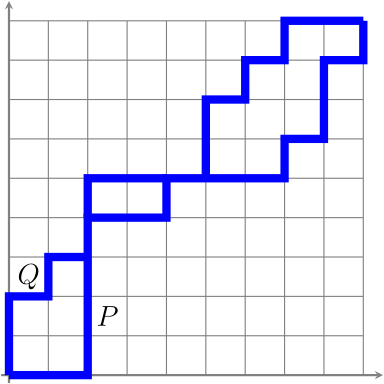
Let $P$ and $Q$ be two lattice paths to $(a,b)$. We say that $P \le Q$ if $P$ never goes above $Q$; this defines a partial order on the set of all lattice paths to $(a,b)$. For $P \le Q$, we define the matroid $M[P,Q]$ on $[a,b]$ with set of bases $$\{\mathcal{N}(R) : P \le R \le Q\}.$$

Proposition. $M[P,Q]$ is a matroid.

The matroid $M[P,Q]$ records (the north steps of) all lattice paths between $P$ and $Q$; an arbitrary matroid is called a lattice path matroid if it is isomorphic to $M[P,Q]$ for some $P$ and $Q$. Here are some examples:

• $M[E^aN^b, N^bE^a]$ is the rank-$b$ uniform matroid on $[a+b]$. Here, the first boundary path is the one formed by $a$ east steps followed by $b$ north steps, and the second boundary path is the one formed by $b$ north steps folled by $a$ east steps.
• $M[P,P] \cong U_{b,b} \oplus U_{0,a}$ for any lattice path $P$ to $(a,b)$.
• $M[E^nN^n, (EN)^n]$ is the Catalan matroid with exactly $\frac{1}{n+1}\binom{2n}{n}$ bases.

Properties of $M[P,Q]$ can (in principle) be explained in terms of $P$ and $Q$ alone. We will need the following result later.

Proposition. The element $i$ is a coloop of $M[P,Q]$ if and only if $P_{i-1} = Q_{i-1}$ and $P_i – P_{i-1} = Q_i – Q_{i-1} = N$. The element $i$ is a loop of $M[P,Q]$ if and only if $P_{i-1} = Q_{i-1}$ and $P_i – P_{i-1} = Q_i – Q_{i-1} = E$.

An attractive property of the class of lattice path matroids is that it is closed under duality and minors. Both of these operations have interpretations in terms of lattice paths.

Duality

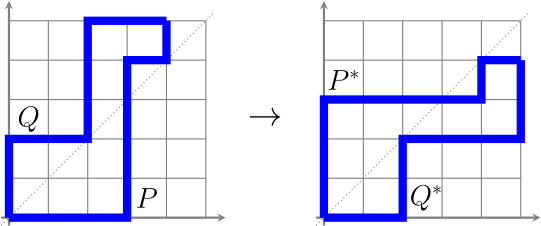
Let $\mathcal{N}(R)$ be a basis of $M[P,Q]$. Then the complement of $\mathcal{N}(R)$ in $[a+b]$ is a basis of the dual matroid $M[P,Q]^*$: its elements correspond precisely to the east steps in $R$. This inspires the following definition.

For a lattice path $R$, let $R^*$ be the lattice path obtained from $R$ by flipping the roles of north and east steps. If $R$ is a lattice path to $(a,b)$, then $R^*$ is a lattice path to $(b,a)$. Geometrically, $R^*$ is obtained from $R$ by reflecting it in the line $y=x$. It is clear from the geometric perspective that if $P \le R \le Q$, then $Q^* \le R^* \le P^*$, from which it can be shown that the dual of $M[P,Q]$ is again a lattice path matroid.

Proposition. $M[P,Q]^* = M[Q^*, P^*]$.

Minors

Showing that the class of lattice path matroids is minor-closed requires a bit more work. Fortunately, in view of the previous result, it suffices to show that deleting a single element from $M[P,Q]$ results in a new lattice path matroid.

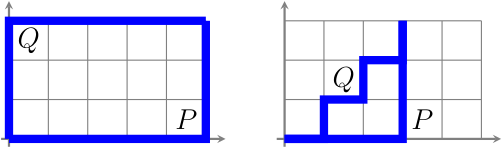
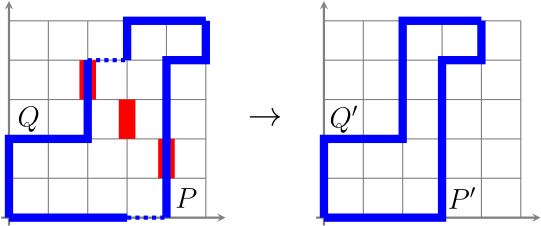
So let $M = M[P,Q]$ be a lattice path matroid and let $i$ be an element of $M$. If $i$ is a loop or coloop of $M$, then $P$ and $Q$ coincide in the $i$-th step; a lattice path representation can be obtained from $P$ and $Q$ by deleting this step from both paths. (When drawing $P$ and $Q$ in $\mathbb{Z}^2$, the resulting disconnected parts of the lattice paths should be connected up again by “sliding” the north-east component one unit to the south (when $i$ is a coloop) or to the west (when $i$ is a loop).)

When $i$ is neither a loop nor a coloop, the bases of $M\backslash i$ are the bases of $M$ that do not contain $i$. In terms of lattice paths, this means that the lattice paths $R$ corresponding to bases of $M\backslash i$ satisfy $P \le R \le Q$ and $R_i – R_{i-1} = E$: we disallow north steps starting from any point $(u,v)$ such that $u+v=i-1$. We obtain lattice paths $P’$ and $Q’$ representing $M\backslash i$ by “merging” the two squares on either side of such north steps. More precisely, we obtain $P’$ from $P$ by deleting the last east step at or before the $i$-th step, and $Q’$ from $Q$ by removing the first east step at or after the $i$-th step. See the figure for an illustrative example.

Proposition. $M[P,Q]\backslash i \cong M[P’,Q’]$.

We conclude that the class of lattice path matroids is closed under taking minors. Joe Bonin identified the excluded minors for the class of lattice path matroids: they comprise the rank-3 wheel and whirl, a rank-3 matroid on seven elements called $R_3$ and its dual, and five infinite families.

The class of lattice paths has many more interesting properties. For example, all of them are transversal matroids and their Tutte polynomials can be computed in polynomial time. I refer to the original papers by Bonin, De Mier, and Noy for this and more.

Colouring and list-colouring

Staying close in theme to last month’s post, this month I’m writing about decomposing matroids into independent sets.

The colouring number (or covering number), $\text{col}(M)$ of a matroid $M$ is defined as the smallest $t$ for which the ground set of $M$ can be partitioned into $t$ independent sets. I’ve written before about how I like the term colouring number since it highlights the analogy with the chromatic number of graphs (which is the smallest number of vertex-independent sets in which the graph can be partitioned). For this blog post, though, it is more illuminating to compare the colouring number to the edge-chromatic number of a graph.

The chromatic number for graphs has many variations that are studied for their own sake, such as the list-chromatic number. Similarly, there is a list-colouring version of the colouring number, which is defined as follows.

Definition. Let $M$ be a loopless matroid, and suppose that for each element $e$ of $M$ we are given a list $L(e)$ of colours available to element $e$. An $L$-colouring of $M$ is a function $c$ that maps each element $e$ of $M$ to an element of $L(e)$, with the additional property that $c^{-1}(i)$ is an independent set of $M$ for all $i \in \bigcup_{e} L(e)$. The matroid $M$ is $k$-list-colourable if it has an $L$-colouring whenever $|L(e)| \ge k$ for each $e$. We write $\text{col}_\ell(M)$ for the smallest $k$ such that $M$ is $k$-list-colourable.

When $L(e) = \{1,2,\ldots,k\}$ for each $e$, $L$-colouring corresponds to colouring the matroid with $k$ colours. This implies that $\text{col}_\ell(M) \ge \text{col}(M)$. For graphs the gap between chromatic number and list-chromatic number can be arbitrarily large. Surprisingly, the colouring and list-colouring numbers for matroids are equal, as shown by Seymour (using an application of matroid union!).

Theorem (Seymour). $\text{col}_\ell(M) = \text{col}(M)$ for all loopless matroids $M$.

It is clear from this theorem that nothing is to be gained by considering the list-colouring problem for matroids instead of the colouring problem.

However, it is not known if an analogue of Seymour’s result holds for matroid intersections. Let $M_1$ and $M_2$ be two matroids on a common ground set $E$. The colouring number $\text{col}(M_1 \wedge M_2)$ is the smallest $t$ for which $E$ can be partitioned into $k$ sets that are independent in both $M_1$ and $M_2$ (here, $M_1 \wedge m_2$ refers to the matroid intersection of $M_1$ and $M_2$). The list-colouring number for $\chi_\ell(M_1 \wedge M_2)$ is similarly obtained as a generalisation of the list-colouring number for matroids.

As in the case of (list-)colouring matroids, a straightforward argument shows that $\text{col}_\ell(M_1 \wedge M_2) \ge \text{col}(M_1 \wedge M_2)$, but it is not known if equality holds for all matroid intersections.

1-partition matroids and Galvin’s theorem

A 1-partition matroid is a matroid whose ground set can be partitioned into subsets such that the independent sets of the matroid contain at most one element from each of the subsets. In other words, a loopless matroid $M$ is a 1-partition matroid if and only if it is the direct sum of $r(M)$ parallel classes.

Such matroids arise naturally in matching theory. A bipartite graph $G$ with bipartition $L \cup R$ comes with two 1-partition matroids on $E$: one in which the parallel classes are formed by the edges incident with each of the vertices in $L$, and one whose parallel classes similarly correspond to the vertices in $R$. In fact, the matchings of $G$ are precisely the common independent sets of these two matroids.

Galvin showed that the list-edge-chromatic number and the edge-chromatic number of bipartite graphs coincide, which is equivalent to the following result.

Theorem (Galvin). $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$ for all loopless 1-partition matroids.

It is natural to ask if the conclusion of the theorem still holds when the 1-partition matroids are replaced by matroids that are the direct sum of uniform matroids whose rank may be larger than 1 (such matroids are called partition matroids). It turns out that the answer is ‘yes’, a result that was proved only a few months ago by Guo.

Theorem (Guo). $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$ for all loopless partition matroids.

When is $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$?

In light of Seymour’s theorem for the list-colouring number of matroids and the above results by Galvin and Guo, it is tempting to ask whether the list-colouring number is always equal to the colouring number for matroid intersections – as Király did.

Question (Király). Is it always true that $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$?

Very little appears to be known about this problem, with the exception of the results by Galvin and Guo and the following result by Király and Pap.

Theorem (Király and Pap). $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$ in each of the following cases:

• $M_1$ and $M_2$ are both transversal matroids; or
• $M_1$ is the graphic matroid and $M_2$ is the 1-partition matroid whose parts are formed by the in-stars of the graph that is the union of two arborescences with the same root; or
• $M_1$ and $M_2$ both have rank 2.

(The third case of of their result actually extends to the situation where $M_1$ is a rank-2 matroid and $M_2$ is an arbitrary matroid.)

As a step towards resolution of Király’s question, the following problem may be more accessible:

Question. Is it true that $\text{col}_\ell(M_1 \wedge M_2) = \text{col}(M_1 \wedge M_2)$ for all loopless rank-3 matroids $M_1$ and $M_2$?

Happy New Year from all of us at the Matroid Union!

Decomposition of objects into smaller or simpler objects is a central theme in combinatorics. Think about decomposing a graph into its connected components or blocks, or into forests. In today’s post, I discuss decomposing finite projective geometries into projective geometries of smaller rank.

Definition: Let $q$ be prime power, let $n \ge t \ge 1$ be integers and let $M = \text{PG}(n-1,q)$ be the projective geometry over the field with $q$ elements. A $t$-spread of $G$ is a collection of rank-$t$ flats of $M$ that partition the points of $M$—that is, these flats are pairwise disjoint and their union is the set of all points of $M$.

(Geometers often use dimension instead of rank; the dimension of a projective geometry is one less than its rank. Their $t$-spreads are collections of $t$-dimensional subspaces of an $n$-dimensional space. We will however stick to the terminology that is more familiar in the matroid theory setting.)

Every projective geometry has a 1-spread: the flats making up the spread are simply the points of the geometry. It is much more interesting to look into the existence of $t$-spreads when $t \ge 2$.

The Fano plane $F_7 = \text{PG}(2,2)$ does not admit a decomposition into triangles. The quickest argument to see this is based on counting the number of points: any matroid that can be decomposed into triangles necessarily has a number of points that is a multiple of 3, but the Fano plane has seven points. By contrast, the projective geometry $\text{PG}(3,2)$, which has fifteen points, can be partitioned into five triangles (as encoded using different colours in the following representation:

The counting argument above can be generalised. In order for $M = \text{PG}(n-1,q)$ to have any hope of admitting a $t$-spread, the number of points in a projective geometry of rank $t$ should evenly divide the number of points in $M$, or $\frac{q^t-1}{q-1} \bigg| \frac{q^n-1}{q-1}$. It is a nice exercise to show that the latter happens precisely when $n$ is a multiple of $t$. So, if $\text{PG}(n-1,q)$ can be decomposed into rank-$t$ subgeometries, we must have $t|n$.

It turns out that this divisibility criterion is not only necessary—it is sufficient as well. We end this blog post with a slick proof of this fact. The proof can be found in many introductory texts on projective geometry.

Theorem: The projective geometry $M=\text{PG}(n-1,q)$ admits a $t$-spread if and only if $t|n$.

Proof: We already proved the implication from left to right. The implication in the other direction follows from a construction.

Suppose that $n = kt$ for some integer $k$. The points of $M$ can be identified with the 1-dimensional subspaces of the vector space $\mathbb{F}_q^n$. We will show that $\mathbb{F}_q^n$ can be decomposed into $t$-dimensional subpspaces that are pairwise disjoint (except that they all contain the zero-vector). As the 1-dimensional subspaces of $\mathbb{F}_q^t$ can be identified with the points of a $\text{PG}(t-1,q)$, this immediately implies the theorem.

Consider the $k$-dimensional $\mathbb{F}_{q^t}$-vector space $\mathbb{F}_{q^t}^k$. Its 1-dimensional subspaces intersect only in the zero-vector. These 1-dimensional subspaces give us our spread, as each such subspace can alternatively be viewed as a $t$-dimensional $\mathbb{F}_q$-vector space. $\Box$

Tuza’s Conjecture

One of my favourite open problems in Tuza’s Conjecture, which relates triangle packings and triangle hitting sets in graphs.

Let $G$ be a graph. A triangle packing is a set of triangles in $G$ no two of which have an edge in common. The maximum size of a triangle packing is called the triangle packing number of $G$, for which we write $\nu(G)$.

A triangle-hitting set is a subset $X \subseteq E(G)$ with the property that removing $X$ from $G$ results in a triangle-free graph. We write $\tau(G)$ for the size of the smallest triangle-hitting set in $G$.

A straightforward argument shows that $\nu(G) \le \tau(G) \le 3\nu(G)$. Tuza conjectured that the upper bound can be improved.

Conjecture (Tuza, 1981): $\tau(G) \le 2\nu(G)$ for all graphs $G$.

In other words, a graph without $t+1$ edge-disjoint triangles can be made triangle-free by removing at most $2t$ edges.

The factor 2 in the conjecture, if true, is best possible: $K_4$ and $K_5$ are examples for which $\tau(G) = 2\nu(G)$.

Geometric Tuza’s Conjecture

Tuza’s Conjecture, being formulated in terms in terms of edges and triangles only, can be naturally generalised to matroids. A triangle in a matroid $M$ is a restriction isomorphic to $U_{2,3}$. We define $\nu(M)$ to be the maximum number of disjoint triangles in $M$, and $\tau(M)$ to be the minimum size of a set $X$ such that $M\backslash X$ does not contain any triangles.

Unfortunately, the geometric version of Tuza’s Conjecture fails for matroids in general: For the Fano plane, $F_7 = \mathrm{PG}(2,2)$, we have $\tau(F_7) = 3$ and $\nu(F_7) = 1$.

Kazu Nomoto and I believe that, at least for binary matroids, the Fano plane is the only obstruction to a geometric version of Tuza’s Conjecture.

Conjecture (Nomoto–Van der Pol, 2021): Let $M$ be a simple binary matroid with no restriction isomorphic to $F_7$. Then $\tau(M) \le 2\nu(M)$.

As graphic matroids do not have restrictions isomorphic to $F_7$, the geometric version of Tuza’s conjecture implies the graphic version. We verified the conjecture for cographic matroids and several other classes of matroids.

Projective planes

Moving beyond binary matroids, one could ask if Tuza’s Conjecture holds for other classes of matroids. Here, we ask if it holds for projective planes. We’ve already seen that the conjecture fails for the Fano plane. It fails spectacularly for all other finite projective planes as well. This result is closely related to classical results in projective geometry.

A finite projective plane is a set system $\Pi = (E,\mathcal{L})$ — the elements of $E$ are called points, and the elements of $\mathcal{L}$ are called lines — with the following properties:

1. Any pair of distinct points is contained in exactly one line;
2. Any pair of lines intersects in exactly one point; and
3. There are four points such that no line contains more than two of them.

For each finite projective plane $\Pi$ there is a number $q \ge 2$, the order of $\Pi$, such that every point is contained in $q+1$ lines, and every line contains $q+1$ points. It follows that a projective plane of order $q$ contains exactly $q^2 + q + 1$ points.

Well-known examples are the Desarguesian planes $\mathrm{PG}(2,q)$, whose points and lines are the 1- and 2-dimensional subspaces of $\mathbb{F}_q^3$, respectively, but there are other examples as well.

Arcs

The lines in $\mathcal{L}$ form the collection of hyperplanes of a rank-3 matroid on $E$, so it makes sense to talk of $\tau(\Pi)$ and $\nu(\Pi)$ for finite projective planes $\Pi$.

An arc in $\Pi$ is a set $A$ of points such that no line intersects $A$ in more than two points. In our terminology, $A$ is a triangle-free restriction of $\Pi$. (Confusingly, the term triangle is also used for an arc of size 3, which is the opposite of our use of the term.)

The following result is well known in projective geometry.

Lemma: Let $\Pi$ be a projective plane of order $q$ and let $A$ be an arc. Then $|A| \le q+2$. If $q$ is odd, then $|A| \le q+1$.

Proof. Let $p \in A$ be any point, and let $\ell_1, \ell_2, \ldots, \ell_{q+1}$ be an enumeration of the lines incident with $p$. Each point in $\Pi$ is on one of those $q+1$ lines, and each line contains at most one point from $A$ other than $p$, so $|A| \le 1 + (q+1)$.

To prove the second bound, suppose for the sake of contradiction that $q$ is odd and $|A| = q+2$. Every line of $\Pi$ intersects $A$ in either $0$ or $2$ points; this is in particular true for all lines through a fixed point $p \not\in A$. It follows that $|A|$ is twice the number of lines incident with $p$ that intersect $A$, so $|A|$ must be even: a contradiction, so $|A| < q+2$. $\Box$

Arcs of size $q+1$ are called ovals, while arcs of size $q+2$ are called hyperovals. Constructions for ovals and hyperovals exist for the planes $\mathrm{PG}(2,q)$; Segre proved that in $\mathrm{PG}(2,q)$ of odd order, all ovals are nondegenerate conic sections.

By the lemma, sets containing more than $q+2$ points must contain a triangle, so $\tau(\Pi)$ is large.

Lemma: Let $\Pi$ be a projective plane of order $q$. If $q$ is even, then $\tau(\Pi) \ge q^2 – 1$. If $q$ is odd, then $\tau(\Pi) \ge q^2$.

Trivially, $\nu(\Pi) \le \frac{1}{3}(q^2+q+1)$. This is sufficient to show that Tuza’s conjecture fails for projective planes of sufficiently large order, as $\tau(\Pi) \sim 3\nu(\Pi)$ as $q \to \infty$.

The trivial upper bound on $\nu$ is correct, as can be shown by a simple construction.

Lemma: Let $\Pi$ be a projective plane of order $q \ge 3$. Then $\Pi$ can be decomposed into disjoint triangles and at most one point. Consequently, $\nu(\Pi) = \lfloor\frac{1}{3}(q^2+q+1)\rfloor$.

Proof. The exact construction depends on the remainder of $q$ modulo 3. Here, we only give the construction for the case $q = 3k+1$; the case $q = 3k+2$ allows a similar construction, while the case $q=3k$ is easier. See the figure following the proof for an illustration in the case $q=4$.

Let $p \in \Pi$ be any point, and let $\ell_0, \ell_1, \ldots, \ell_q$ be an enumeration of the lines incident with $p$. Let $e \in \ell_0$ be a point distinct from $p$, and let $\ell’ = {e, e’_1, \ldots, e’_q}$ and $\ell” = {e, e”_1, \ldots, e”_q}$ be two distinct lines incident with $e$ such that $e’_i, e”_i \in \ell_i$ for $i = 1, 2, \ldots, q$.

Consider the $(q+2)/3$ disjoint triangles

$\{e’_2, e’_3, e’_4\}, \{e’_5, e’_6, e’_7\}, \ldots, \{e’_{q-2}, e’_{q-1}, e’_q\},\quad\text{and}\quad\{e,e”_1, e”_2\}$,

and let $Z$ be the set of all points in those triangles. $Z$ contains exactly one point on each of the lines $\ell_i$, except that it contains two points of $\ell_2$. It follows that each of the sets $\ell_i\setminus (Z \cup {e})$ (for $i \neq 2$) and $\ell_2\setminus Z$ can be partitioned into triangles. $\Box$

It follows from the above results that

$\frac{\tau(\Pi)}{\nu(\Pi)} \ge \frac{q^2-1}{\frac{1}{3}(q^2+q+1)} \ge \frac{15}{7} > 2$

whenever the order $q$ of $\Pi$ is at least 4. For the (unique) projective geometry $\Pi = \mathrm{PG}(2,3)$ of order $q = 3$, we have $\tau(\Pi) = 9$ and $\nu(\Pi) = 4$, while for the (unique) projective geometry $\Pi = \mathrm{PG}(2,2)$ or order $q=2$ we have $\tau(\Pi)=3$ and $\nu(\Pi) = 1$, so Tuza’s Conjecture fails for all finite projective planes.